原文作者：Weikeng Chen

在以太坊虚拟机（EVM）中，Keccak 哈希函数广泛用于状态树（Merkle Patricia Trees）的构造与验证，占据了零知识证明中的主要计算开销。如何高效地对 Keccak 进行证明，是零知识证明领域长期未解的技术难题。

为应对这一挑战，Polyhedra 团队推出了 Binary GKR——一种专为 Keccak 及其他二进制操作设计的高性能证明系统。

核心进展：对 Keccak 的证明速度提升 5.7 倍

Binary GKR 实现了迄今为止最快的 Keccak 零知识证明性能，相比现有二进制证明系统最优解 FRI-Binius 提速约 5.7 倍。这一突破不仅在理论上具有重要意义，也为实际应用打开了新的可能性。

应用前景：zkEVM 的“通用加速侧车”

我们认为，Binary GKR 可作为多种 zkEVM 架构中的“通用加速侧车”，高效处理 Ethereum 状态树中大量的 Keccak 运算，从而显著降低证明成本、提升系统吞吐与响应速度。

Polyhedra 将持续推动 Binary GKR 的产品化与开源进程，赋能以太坊及更广泛生态中的 zk 架构升级。

Keccak：零知识以太坊的“圣杯”

以太坊正逐步向零知识证明原生的 Layer-1 演进。由 21 个团队参与、涵盖 22 种 ZK(E)VM 实现的 Ethproofs 计划，正在尝试对以太坊历史区块进行完整证明，迈出关键一步。

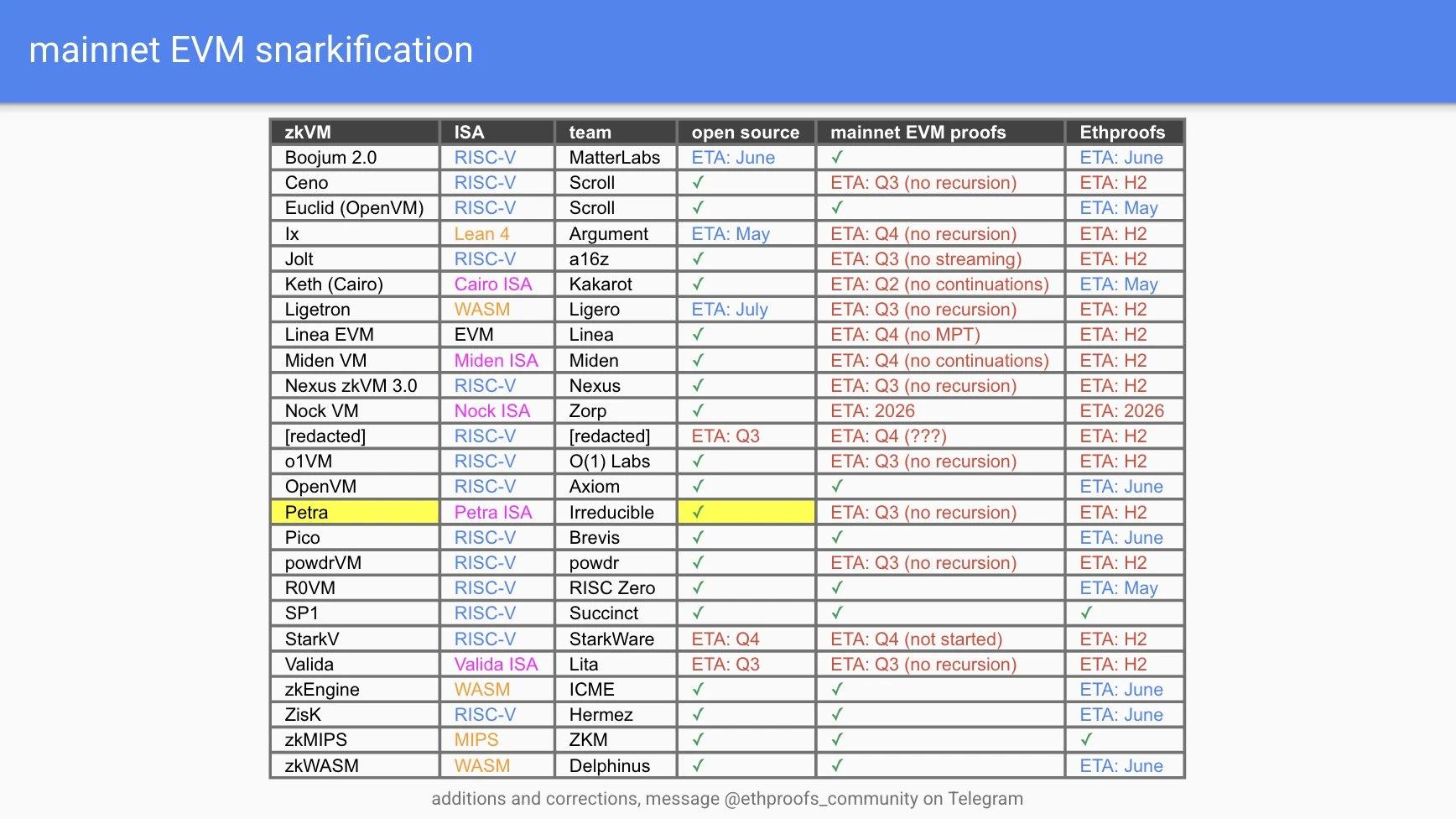
在 Ethproofs 官网 上可以实时查看多个团队的进展：ZkCloud、Succinct、Snarkify 和 ZKM 等项目，已开始持续提交最新区块的 ZK 证明。这一趋势的最终目标，是将以太坊打造为以零知识证明驱动的执行层，而共识层仅需完成交易列表的提议等轻量任务。

zkEVM 架构面临的最大挑战：Keccak 的证明效率瓶颈

目前已有多个以太坊兼容 zkRollup 项目（如 Polygon、Taiko、Scroll）尝试实现 zkEVM。然而，传统 EVM 中一些在 CPU 上高效的操作，在零知识证明系统中却代价高昂。其中最主要的性能瓶颈，正是 Keccak 哈希函数。

Keccak 被广泛用于构建以太坊的 Merkle Patricia Tree，以哈希形式记录全链状态。然而 Keccak 的底层运算基于 位运算（bit-level operations），这与大多数 ZK 系统使用的 素数域（prime field）运算模型 并不兼容，从而导致性能显著下降。

为了帮助理解 Keccak 哈希函数为何本质上是“位运算”的集合，我们在此简要展示其中的五个核心操作：θ（theta）、ρ（rho）、π（pi）、χ（chi）和 ι（iota）。这些操作应用于一个 5 × 5 的矩阵结构，每个单元格为一个 64 位整数，我们称之为“字”（word）。整个矩阵共包含 5 行 5 列。

• θ（Theta）：首先计算每一列的奇偶校验值（parity），然后将该奇偶值与左侧相邻列进行异或运算（exclusive-or）；同时，对右侧相邻列执行一次左旋转（rotate-left）后，再进行异或。这一过程涉及基本的二进制操作，如“异或”与“左旋”。

• ρ（Rho）：对矩阵中的每一个字按位左旋转，每个字的旋转距离不同，但均为预设的固定值。该步骤完全由“左旋”操作构成。

• π（Pi）：根据固定模式重新排列矩阵中的字。由于该过程仅为位置置换，在零知识证明中通常被视为“零成本操作”。

• χ（Chi）：沿每一行进行按位组合操作，每个字会与该行中其左右相邻的两个字进行组合。该操作包括“异或”、“取反”（negation）与“与”（and）。

• ι（Iota）：将矩阵中第一个字与一个固定常数进行异或操作，仅涉及“异或”运算。

在零知识证明中实现 Keccak 的主要挑战，正是如何有效表示这些位级操作，尤其是在每个操作都作用于 64 位整数的前提下。这也是我们称其为 Keccak-1600 的原因——因为每一轮的状态空间为 5 × 5 × 64 = 1600 位。而这样的操作过程需重复 24 轮。

接下来，我们将简要回顾一些此前实现 Keccak 的尝试。

尝试一：基于 Groth 16 或其他 R 1 CS 的证明系统

目前最流行且最直接的方式，是使用 Groth 16 或其他 R 1 CS（Rank-1 Constraint System）证明系统来实现 Keccak。为了在 Groth 16 中表达位运算，我们将每个位表示为 0 或 1 ，并通过算术关系来模拟如下逻辑运算：

• 异或（exclusive-or）：使用表达式 a + b − 2 ab

• 取反（negation）：使用表达式 1 − a（通常可无成本地融合进其他约束中）

• 与（and）：使用表达式 a × b

而像“左旋”（rotate-left）和其他置换操作在 ZK 环境中通常被视为无成本操作，不需要额外约束。

根据计算，Keccak 每一轮中的约束数量如下：

• θ 操作约产生 4480 个约束

• ρ 与 π 操作为“零成本”

• χ 操作约产生 3200 个约束

• ι 操作约产生 64 个约束

因此完整的 Keccak-1600 （共 24 轮）将在 Groth 16 中产生 185, 856 个约束。

参考 Ingonyama 的 ICICLE 库中的数据，在一块 Nvidia 4090 GPU 上生成一个 Keccak 的 ZK 证明大约需要 30-40 毫秒，在 CPU 上则约为 450 毫秒。如果需要证明 8192 次 Keccak 运算，GPU 至少需要 250 至 300 秒，而 CPU 可能需要接近 一小时。

尝试二：基于查找表的证明系统（Lookup-based Proof Systems）

一种更现代的优化方案是对数据进行批量处理（例如每 4 位或 8 位一组），并通过查找表来执行所有的位运算。换句话说，将每个 64 位整数切分成若干小块（例如 8 个 8 位 chunk），再使用查找表完成逻辑操作。

具体包括以下几种查找表：

异或操作查找表（XOR）：一个大小为 2 ⁸ × 2 ⁸ 的查找表，用于计算两个 8 位 chunk 的异或值。这样可以用一个约束完成 8 位异或，而不是传统的 8 个约束。

与操作查找表（AND）：同样是一个 2 ⁸ × 2 ⁸ 的查找表，用于两个 8 位 chunk 的按位与操作，节省约束的效果与 XOR 类似。

左旋操作查找表（Rotate-left）：为了处理 Keccak 中频繁出现的 rotate-left 操作，引入了多个查找表。具体为：七个大小为 2 ⁸ 的查找表，分别对应旋转距离为 8 k+ 1、 8 k+ 2 等（其中 k 为非负整数）。相较于尝试一（Attempt 1）完全不处理旋转操作，这种方式会引入额外开销——每轮大约增加 192 个约束。不过与其他部分相比，这个开销仍然相对较小。

为了实现这种系统，我们不再使用 Groth 16 ，而是更适合采用 Stwo、Plonky 3 等小域证明系统，这类系统对查找表支持更加完善。在该方案下，每次完整的 Keccak 运算大约需要 27, 264 个约束，并结合查找表的调用，可大幅减少整体约束数，相较 Groth 16 显著优化。

然而，这种优化在性能上并非绝对占优。因为查找表本身的调用和管理也会带来开销，若处理不当，可能抵消约束数量减少所带来的优势。因此，其实际运行效率在某些场景下可能不如基于 Groth 16 的实现。

尝试三：Binius

鉴于查找表（lookup）或定制门电路（customized gates）所带来的加速在实际中可能不及预期，原因在于查找本身的开销可能抵消其带来的约束优化效果，因此我们需探索其他路径来进一步提升 Keccak 的证明效率。

这正是 Keccak 被誉为“零知识圣杯”的原因所在。与之相比，早期的哈希函数如 SHA-256 和 Blake 2/3 ，虽也依赖于异或（XOR）、与（AND）等位运算，但其最大性能瓶颈源于整数加法。而整数加法在证明系统中通常通过将其拆解为多个 4-bit 块来优化，从而大幅提升性能。但 Keccak 并不涉及任何整数加法，因此这些优化策略在此处失效。

目前最前沿的解决方案是 Binius。该系统的核心思想是：既然 Keccak 完全由位运算组成，我们便可以使用以 位为基本单位 的证明系统来实现。这便是 Binius 的突破之处。

在 Binius 中，Keccak 被表示为在有限域